|
|
踢足球的鼠标 · TiN0.3/AlN复合烧结界面扩散现象· 2 月前 · |
|
|
踢足球的鼠标 · Si中掺杂原子的瞬间增强扩散现象及抑制方法· 2 月前 · |
|
|
踢足球的鼠标 · 油扩散泵|真空泵(高真空)的基础知识|技术知 ...· 2 月前 · |
|
|
踢足球的鼠标 · 通过拉曼光谱对扩散现象表征- HORIBA· 2 月前 · |

空气中的二氧化碳(CO 2 )或咖啡中的糖等化学物质,即使处于静止状态,一段时间后也会与周围的流体完全混合。热量也会通过静止的物体在同样的传输机制下传递,直到温度变得均匀为止。类似地,在存在摩擦的流体层中,作用于流体表面上力会在流体层的整个厚度上传递。在流体环境中,湍流能促进其组分的分散,但是这种分散并没有达到分子的尺度。正是这种分子的无序运动才完成了这一我们称之为扩散的输运过程。我们还发现,分子扩散是一个非常缓慢的过程,但湍流能显著促进扩散。
“ diffusion ”一词的含义不尽相同,但所有解释的共同点是:某种量通过介质基本组成粒子的搅动而分散到周围介质中的输运过程。在物理学中,我们要区分下面两种类型的扩散现象:
在日常用语中,“ diffusion ”一词也有不同的含义,它既可以指对公众的知识的传播,也可以指通过无线电(无线电广播)或电视(电视广播)实现各种类型的信息传递。
1. 静止的空气:一群躁动不安的分子
文章 《地球的大气层和气体层》 中提到,干燥空气的主要成分有氮气(71%)、氧气(28%)、氩气(少于1%),还有其他含量更少的气体。气体分子会充满所有可用的空间,这是气体有别于其他凝聚态物质(液体或固体)的一种属性。固体或液体有特定的体积,固体还有自己固定的形状。
[来源:© 瑞内·莫罗(René Moreau)]
2. 气体的分子参数与宏观属性之间的关系
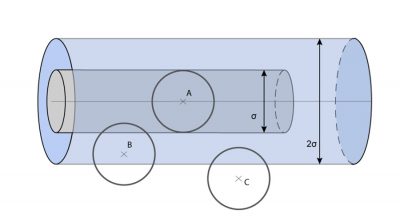
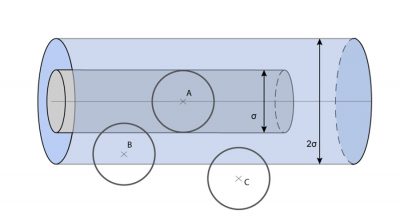
通过感知和测量,我们可以很容易地将分子世界的这些参数与一些宏观量相关联。 《压强、温度和热量》 一文对压力 p ,温度 T ,单位体积的质量(密度) ρ 和粘度 [3] μ 这些物理量之间的关系已经做了分析,从中我们可以得到分子尺度与宏观尺度之间的 第一个关系 : m = M / N A , N A = 6.022×10 23 mol -1 ,即每个分子的质量 m 等于摩尔质量 M 除以阿伏伽德罗常数(每摩尔中的分子数)。并且密度 ρ 等于单位体积中的分子数量 n 乘以每个分子的质量,这样我们就得到了两种尺度参数之间的 第二个关系 : ρ = nm 。
为了将气态介质中某一点的压力 p 与气体分子的参数联系起来,我们假设在该气态介质中的某处有一个单位面积的固平面( S = 1,单位可任意选择)。单位时间内该平面的两侧会不断地受到气体分子从各个不同方向的撞击和动量积累,在这一过程中气体分子失去并重新获得动能,每个分子的动能为 mc 2 / 2 。由此,施加在单位表面上的压力 p 平均为 nmc 2 。考虑到气体分子的真实速度 [4] 和实际相撞速度,经严格的推算可得到压力的表达式为 p = nmc 2 /3,其中系数1/3修正了由于我们简化模型估算而带来的误差。从而我们得到了气体分子参数( n , m , c )和宏观属性(压力 p )之间的 第三个关系 。
由上面的几个关系式我们知道压力和密度都与分子的参量相关,可由理想气体状态方程表示出温度与压力的关系: p / ρ = RT / M ,其中 R = 8.314 m 3 ·Pa·mol -1 ·K -1 , R 为理想气体常数, M 为气体混合物的平均摩尔质量。这样我们就得到了 第四个关系式 [5] : T = Mc 2 /3 R ,这个表达式强调了温度 T 和分子的速度平方 c 2 之间的正比例关系(详见文章 《压强、温度和热量》 )。
除此之外,还有一个表示气体动力学粘度的关系式: μ = nmcλ /3,这个关系式将会在本文第5节中说明。由此, 海平面处的空气 ,通常具有以下值:
p = 1.01310 5 Pa , T = 288 K , ρ = 1.22 kg·m -3 , ν = 10 -5 m 2 ·s -1 ,
由上述的五个关系式可以得到:
n = 2.510 25 m -3 , m = 4.810 -26 kg , c = 497 m·s -1 ,
d = 3.410 -9 m , σ = 0.4610 -9 m , λ = 610 -8 m 。
为了对分子世界的尺度有一个更准确的认识,我们可以从上述计算结果中得知,边长为1微米的小立方体包含约2500万个气体分子,且两个相邻分子之间的距离( d )约为其直径( σ )的7倍,平均自由程( λ )约为60 nm,是分子直径的130倍,并且分子的平均速度( c = 497 m·s -1 )比声速(340 m·s -1 )略高。
3. 气体扩散机制
[来源:© 瑞内·莫罗(René Moreau)]
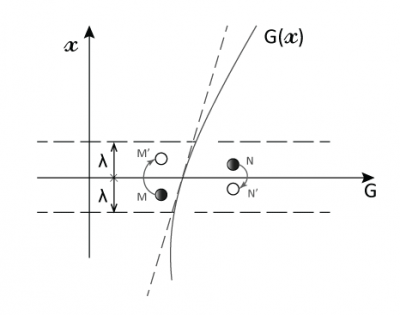
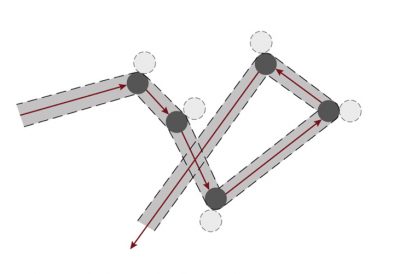
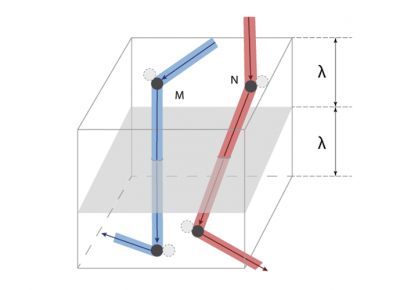
然而,建立这种平衡所需的时间比分子两次碰撞的间隔时间( λ / c ≈ 1.4×10 -10 s)长得多(几小时或更久)。因此在非平衡状态下气体分子的碰撞会非常频繁,如果碰撞后的分子都具有相同的 G 值,即 G / n ( G 为单位体积的值),我们就说气体处于 局部平衡 的状态。
穿过平面 x = 0(如图3)的分子的 G 值平均为 G / n , 其运动距离约等于平均自由程 λ 。因为与宏观尺寸相比 λ 极小,所以 G(x) 在 x = 0附近可用其斜率为 Γ 0 的切线替代,这样就可以得到一个简单的分布: G = G 0 + Γ 0 x 。我们进一步假设:对于来自 x > 0侧的分子 G + = G 0 + Γ 0 λ ,对于来自 x <0侧的分子 G – = G 0 – Γ 0 λ 。
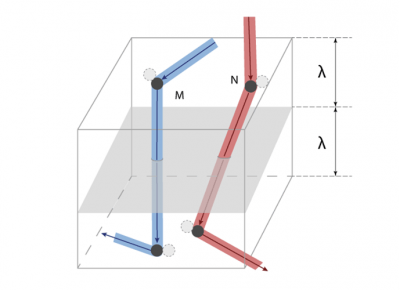
[来源:© 瑞内·莫罗(René Moreau)]
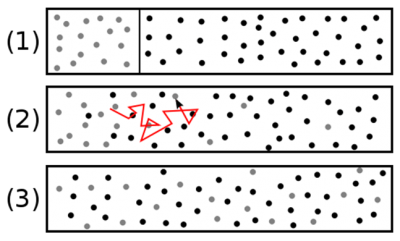
要估算 G 通过该单位面积截面的净流量,须将 G 的前后之差 γ 0 λ 乘以单位时间内穿过该截面的分子数。在该单位面积上方的体积中(如图5),有 nλ 个分子,每个分子在单位时间内发生 c / λ 次碰撞,所以在该体积内单位时间发生的碰撞次数约为 nc 。但是只有碰撞后朝向该截面的分子才会穿过该面,由此进一步计算得出单位时间内穿过该截面的分子数为 nc /3(系数也是1/3)。
最后,可以通过关系式 φ = (cλ/3)dG/dx 来估计平面 x = 0上单位面积的 G 的流量 φ 。由此我们可以得到如下结论:如果 G 的分布不均匀,则 通过分子搅动传输的 G 的净流量与该区域 G 的局部梯度 d G /d x 成正比 ,可以用 φ = -DdG/dx 表示。通常,我们在式中加上负号“-”,这样当 dG/dx 为负时(比如热量从热侧流向冷侧),流量则为正。其中系数 D = cλ / 3,称为气体的 扩散系数 ,它是纯粹的运动学参量,单位是m 2 /s。扩散系数反映了气体扩散能力的大小,与气体自身的性质无关。
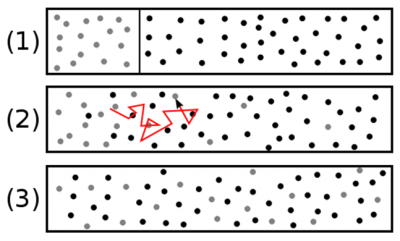
用第2节中给出的数值可以估算出空气的扩散系数。当 c = 497 m·s -1 和 λ = 6×10 -8 m时,可得出 D ≈ 10 -5 m 2 ·s -1 。为了使该数值更具有实际意义,让我们回到图4所示的实验中:设容器的长度为 L ,因为扩散系数是长度的平方除以时间( L 2 T -1 ),所以达到最终平衡状态所需时间为 L 2 / D 。如果 L ≈ 10cm,则扩散持续的时间约为一个小时。倘若要使这个过程的持续时间约为1秒,则图4中的容器长约为1毫米,与小气泡相仿。
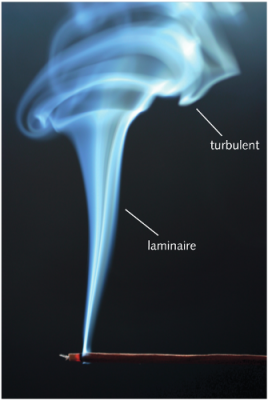
4. 湍流扩散
我们在生活中遇到的大多数流体中,如空气和水,湍流几乎是无处不在的。这是一种与分子运动完全无关的紊乱现象。在诸如风或洋流之类的流动中,湍流大范围存在,有显著的、可测量到的速度脉动。即使没有强加的流动,仅由于流体的动力学不稳定性 [6] ,湍流也会以一系列大小不一的涡的形式存在。这与前面几节所谈到的分子搅动有相似之处,然而,宏观涡的大小要远大于分子的平均自由程,于是普朗特(Prandtl) [7] 定义了一个新的量: 混合长度 [8] ,类似于气体分子的平均自由程。
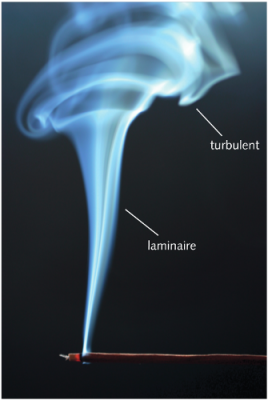
[来源:© 克鲁诺斯拉夫·克内泽维奇(Krunoslav Knezevic)]
混合长度的概念非常模糊,但它的数量级却可以有很高的精确性,特别是存在边界层的情况下(如图7所示)。普朗特(Prandtl)提出在边界层内混合长度的表达式为 l = κy ,其中 y 是到边界的距离, κ 是根据不同条件确定的常数。有了混合长度 l 的表达式,就可以用 u’ ≈ l d U /d y 估算距边界为 y 处速度脉动的量级。类比气体扩散,引入了类似分子扩散系数( D = cλ /3)的概念,用 u’ 代替 c 、 用 l = κy 代替 λ , 则边界层内的湍流扩散系数 D t 为: D t ≈ u’l ≈ κ 2 y 2 d U /d y 。
举例来说,在我们所处的厚度约为几百米的大气边界层内,距地面 y ≈ 10 m处,假设空气的平均速度约为10 m·s -1 ,d U /d y ≈1 s -1 ,由实验得到的常数κ的值为0.1,则可计算出湍流的扩散系数 D t ≈ 10 m 2 ·s -1 ,它是分子扩散系数的一百万倍。所以 获得湍流混合物所需的时间约为十分之一秒 : t ≈ l 2 / D t ≈ 0.1s。但是这种混合是不完全的,因为各成分仅能扩散到最小的涡的尺度,这个尺度取决于流体的粘度。在大气中,边界层的厚度约为1毫米。我们知道 分子搅动达到分子尺度的混合 所需要的时间为 L 2 / D 。在现实中,分子扩散达到毫米尺度时就开始于与湍流的涡的扩散并存了。由此我们可以进行简化,假设分子扩散仅在毫米量级以下起作用。当 L ≈ 10 -3 m, D ≈ 10 -5 m 2 · s -1 时,我们得到 扩散的时间尺度仍 为十分之一秒 左右。
从这些估算中我们可以得到如下结论:
5. 质量扩散和热扩散
通常用质量扩散率来表示化学物质在其所处流体中的扩散。假设流体(气体或液体)中的某些分子与其它分子不同,例如气态的水分子(H 2 O),处于较大的液体区域(例如宁静的湖泊)上的静止空气中。记 C 为在任一高度 z 下空气中水的体积浓度。参照上面推导出的公式,水蒸气向高海拔处扩散的净流量的表达式为 φ = – D d C /d z ,这就是 菲克定律 。要计算出水从低海拔处质量扩散的量,还要补充质量平衡以及初始条件和边界条件。
热扩散率 的表达式是由通过分子搅动进行热传递的过程推导得来。假设 G 是气体单位体积的内能 E ,则有d E = ρC v d T ,其中d T 表示无穷小的温度变化量, C v 为气体的定容热容。所以内能,即热量的扩散传输可表示为 φ = – ρC v D d T /d z 。通常将该等式的以下两种形式都称为 傅立叶定律 : φ = – k d T /d z (其中 k = ρC v D = C v nmcλ /3为气体的 热导率 );或 φ = – αρC p d T /d z (其中 α = k / ρC p 为气体的 热扩散率 , C p 是气体的定压热容)。
上述气体,特别是空气的物理性质( D , k , α , μ , ν )与分子参数 n , m , c 和 λ 有关。其中,对于给定密度的气体,只有分子的速度 c 可能随温度 T 变化,可以表示为: T = Mc 2 /3 R = mc 2 /3 kB 。由此可以推断出 气体的扩散系数 ( D , k , α , μ , ν ) 随着其温度的平方根一同变化 。
6. 动量扩散:粘度
假设上述概念对沿着壁面流动的宏观流体仍然适用。只要这个宏观流动的时间(通常为数秒或数分钟)远大于分子两次碰撞间隔的时间(约10 -11 s),就可以证明这个假设是正确的。

当 z = 0不是壁面与流体的界面,而是两个流层之间的界面时,上面的结论也同样适用。当两个流层之间的界面以速度 u 流动时,牛顿粘性定律也可以表示流层之间相互作用的切向力,通常称之为 摩擦力 。这个沿速度方向的切向力会与和界面垂直方向的压力叠加(详见 《压强、温度和热量》 )。
7. 液体中的扩散机制
实际上所有液体都有自己的体积,这说明组成它们的分子彼此靠得很近。相邻分子之间的平均距离取决于施加在该液体上的压力,分子间距在通常情况下( p ≈ 10 3 hPa)比分子尺寸稍大,为10 -10 ~10 -9 m。这些分子的热运动,或称分子振动,使液体介质具有了一定的扩散能力,但是其扩散能力远弱于气体。这主要是因为液体中分子的作用半径小于其自身大小,而在气体中分子的作用半径即平均自由程,约为分子大小的25倍。这就解释了为什么在咖啡里加糖后需要用勺子搅拌。
存在于液体介质中的任何与介质分子不同的粒子都会不断地受到整体振动的影响,与气体介质中类似,这些粒子会从多的一侧流向少的一侧。该通量仍可以用菲克定律来表示:φ = -DdC/dx,其中D表示液体中粒子的扩散系数,C为其体积浓度。
为了了解液体的 质量扩散率 ,从而反映其传输另一种物质的能力,爱因斯坦在1905年提出了如下定律 [11] : D = k B T / 6πμr ,其中 k B = 1.38×10 -23 J·K -1 是玻尔兹曼常数, T 是绝对温度, μ 是液体的动力粘度, r 是被输运粒子的半径。在一个 r ≈10 -9 m、 μ ≈10 -3 Pa·s的液体环境中,例如水,当环境温度为300 K时,我们得到 D ≈ 2×10 -10 m 2 ·s -1 ,比气体的扩散率小了约10000倍。爱因斯坦的公式中含有温度 T ,这表明分子热运动是扩散背后的真正驱动力。而分母中包含 μ 和 r 则意味着粘度与扩散率呈反比例关系,粒子的半径越大,扩散就越困难。
对于水和所有电绝缘液体而言,它们的热扩散率和质量扩散率差不多。但是 对于液态金属 来说,电子的热传导也是一种主要的传热机制,比质量扩散要重要得多。最著名的例子是液态钠用于冷却超再生器型核反应堆,如“凤凰号”,这一反应堆位于马尔库尔(Marcoule),1973年至2010年期间一直在运行。在300 K左右的温度下,液态钠的热扩散系数约为7×10 -5 m 2 ·s -1 ,比它的质量扩散率要高出10000倍。
8. 总结
参考资料及说明
封面图片: 在日出之前乡村宁静止的空气中,植被呼吸作用释放的物质通过扩散作用传输到空气中。
[1] 纳米是米的十亿分之一(10 -9 m),微米是米的百万分之一(1μm= 10 -6 m)
[2] 路德维希·玻尔兹曼(Ludwig Boltzmann,1844-1906),奥地利物理学家、哲学家,提出了一种名为“硬球”的分子模型,由该模型推导出了一个以他名字命名的方程。
[3] 通常用运动粘度 ν 代替,运动粘度 ν 是动力粘度 μ 与密度 ρ 之比,即 ν = μ / ρ 。
[4] 所有这些速度矢量,包括其各自的方向和值,都可用麦克斯韦分布函数表示。但计算较复杂,超出了本文涉及的范围。
[5] 通过引入与R相关的玻尔兹曼常数 k B 和阿伏伽德罗常数 N A = 6.0248×10 23 , k B = R / N A = 1.380×10 -23 J/ K,该表达式可更好地表示为 k B T = mc 2 /3(焦耳热用开氏温度表示)。
[6] 例如在黎明时太阳升起,地表开始变暖,地面就会通过热扩散加热最低层的空气,使低层的空气比上方的空气更轻。这种较重流体位于较轻流体上方的情况是不稳定的。
[7] 路德维希·普朗特(Ludwig Prandtl,1875-1953),德国物理学家,慕尼黑大学教授,对流体力学做出了重要贡献。他以边界层理论、混合长度的概念和有限翼展机翼升力计算的简单理论而著称。
[8] Lesieur, 湍流(Turbulence), 法国EDP Sciences出版社, 格勒诺布尔科技出版社(Grenoble sciences collection), 2013, p. 128.
[9] 通过建立位于壁面 z > 0侧的小的气域的整体平衡,得出 φ = – τ ,该小气域对流体施加- τ 的切向力,这种整体平衡的表述通常称之为 动量定理 。
[10] 这种表述是由纳维叶(Navier)和傅里叶(Fourier)等人建立的(详见《扩散之父》(《Fathers of the diffusion concept》))。
[11] 阿尔伯特·爱因斯坦(Albert Einstein),布朗运动理论的研究(Investigations on the Theory of the Brownian Movement),多佛出版社(Dover Publications),Inc. (1985), (ISBN 0-486-60304-0). 重新发行了爱因斯坦关于布朗运动理论的原文。
环境百科全书由环境和能源百科全书协会出版 ( www.a3e.fr ),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René (2024年4月12日), 扩散,充分混合过程中极为关键的一步, 环境百科全书,咨询于 2024年9月13日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/zh/physique-zh/diffusion-ultimate-step-good-mixture/ .
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。
文章目录
要了解更多关于它的信息

Chemical species such as carbon dioxide ( CO2 ) in the air, or sugar in coffee, end up, after a while, being intimately mixed with the surrounding fluid, even if it is at rest. The same mechanism transports heat through the stationary bodies until their temperature is uniform. Similarly, in a fluid layer subjected to friction, the force exerted on the surface is transmitted in its full thickness. In fluid environments, turbulence disperses the constituents, but does not reach molecular scales; it is the disordered agitation of molecules that completes this transport process called diffusion. We will see that it alone would be extremely slow but that turbulence helps it effectively.
The word diffusion is used with relatively varied meanings. What is common to all situations is the fact that a certain quantity is transported through a medium dispersed by the agitation of the elementary particles that constitute it. In physics, we distinguish two families of diffusion phenomena:
In everyday language, the same word, diffusion , is used with even different meanings. Thus, it can refer to the transfer of knowledge to a large number of people; it can also refer to the transmission of various types of information by radio (called radio broadcasting) or television (called television broadcasting).
- 1. The air at rest: an agitated set of molecules
- 2. Molecular parameters with macroscopic properties of a gas, or the reverse
- 3. The mechanism of diffusion in gases
- 4. The turbulent diffusion
- 5. Mass and thermal diffusion
- 6. Diffusion of movement: viscosity
- 7. The mechanism of diffusion in liquids
- 8. Messages to remember
1. The air at rest: an agitated set of molecules
In the article The Earth’s Atmosphere and Gaseous Envelope , the main components of dry air are mentioned: nitrogen (71%), oxygen (28%), argon (less than 1%), as well as some other gases in much smaller proportions. This set is made up of molecules, which occupy all the available space, a specific property of gases, which distinguishes them from the condensed states of matter (liquid or solid). These have their own volume, the solids also having their own shape.
2. Molecular parameters with macroscopic properties of a gas, or the reverse
It is quite simple to link these parameters of the molecular world to some macroscopic quantities, measurable and accessible to our senses. These quantities – analyzed in the article Pressure, Temperature and Heat – are pressure p , temperature T , mass of the volume unit (or density) ρ and viscosity [3] μ For this purpose, we have an almost obvious first relationship between molecular and macroscopic scales: mass m is the quotient m = M/NA between the molecular weight M and the Avogadro number (number of molecules per mole) NA = 6.022×1023 mol-1. In addition, the density ρ must be equal to the product of the number n of molecules present in the volume unit multiplied by the mass of each molecule. We therefore have a second relationship between the parameters of the two worlds: ρ = nm .
To connect the pressure p at a point in the gaseous medium to its molecular parameters, let us imagine that a flat solid surface of unit area (S = 1 , whatever the chosen system of units) is placed somewhere in this gaseous medium. Each of the two sides of the surface will receive and accumulate the impulses of all the molecules that will hit it during the unit of time, coming from all directions, losing and regaining their kinetic energy, in the order of mc2/2 for each of them. On average, the force exerted on the unit surface and equal to p must therefore be of the order of nmc2 . A rigorous calculation, taking into account the real velocities of the molecules encountered [4] , would lead to the expression p = nmc2/3 . In passing, we obtain an evaluation of the error due to the simplifying assumptions of the model adopted: the coefficient 1/3 . The important thing here is that we have obtained a third relationship between the molecular parameters (n, m, c ) and a macroscopic property, the pressure p .
Since pressure and density are related to molecular parameters, it is sufficient – to express temperature – to identify the pressure p expressed above with the one that verifies the state equation of perfect gases: p/ρ = RT/M , where R = 8.314 m3 .Pa.mol-1.K-1 denotes the universal constant of perfect gases and M the average molar mass of the gas mixture. We obtain the fourth relationship [5] T = Mc2/3R which highlights the proportionality between the temperature T and the square of the velocity of the molecules c2 (Read Pressure, Temperature and Heat ).
To these four relationships should be added the one that expresses the dynamic viscosity of the gas, which is established later in Section 5: μ = nmcλ/3 . So, with the following values, common for sea-level air
p = 1.013 105 Pa, T = 288 K, ρ = 1.22 kg.m-3, ν = 10-5 m2 .s-1,
the five relationships mentioned above lead to:
n = 2.5 ×1025 m-3, m = 4.8 × 10-26 kg, c = 497 m.s-1,
d = 3.4 × 10-9 m, σ = 0.46 × 10-9 m, λ = 6 × 10-8 m.
To get a fairly accurate idea of the scales of the molecular world, we can see that the number of molecules contained in a small cube of one micron on each side is about 25 million. We will deduce that the typical distance between two neighbouring molecules (d ) is about 7 times their diameter (σ ), that their average free path (λ) is about 60 nanometers, or about 130 times their diameter, and that the average speed of the molecules is slightly higher than the sound velocity (340 m.s-1).
3. The mechanism of diffusion in gases
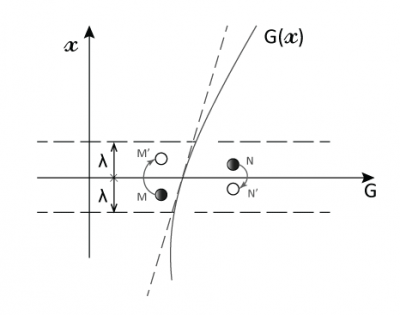
However, the time required to establish this balance is much longer (hours or more) than the time between two molecular collisions (in the order of λ/c ≈ 1. 4×10-10 s). Under these conditions, collisions are so frequent around a given point that it can be assumed that molecules that leave the vicinity of that point after a collision all carry the same value of G , i.e. G/n since G refers to the value per unit volume. It is then said that this gas is in a state of local equilibrium.
Molecules that pass through a flat surface unit perpendicular to the x direction (back to Figure 3) have, on average, the size G/n . The distance from where they come is in the order of an average free journey λ. The smallness of this length λ compared to the macroscopic dimensions justifies assuming linear, with a slope Γ0 , the distribution G(x) in the vicinity of the cut located at x = 0 . This leads to the simple distribution: G = G0 + Γ0 x . Let’s even assume that the molecules that come from the x>0 side all carry G+ = G0 + Γ0λ, and that those that come from the x<0 side carry G- = G0 – Γ0λ.
Finally, the flow rate φ of G through each unit of surface of the plane x = 0 can be estimated by the relationship φ = (cλ/3) dG/dx . The conclusion of this estimate is as follows: if a quantity G is distributed non-uniformly, the net flow of G transported by molecular agitation is proportional to the local gradient dG/dx and is expressed by a relationship of the form φ = -D dG/dx , where, by convention, the sign is placed – so that the flow is positive when dG/dx is negative (heat goes from the warm side to the cold side). The coefficient D appearing in this relationship is D = cλ/3 . It is called the diffusivity of this gas; it is a purely kinematic quantity measured in m2/s. It is remarkable that it was possible to assess the diffusivity of the gas without specifying the nature of the size transported.
The numerical values given in section 2 are used to estimate air diffusivity. With c = 497 m s-1 and λ = 6 × 10-8 m, we obtain : D ≈ 10-5 m2 s-1. To give this value a practical meaning, let us return to the experience in Figure 4: If we note L the length of the enclosure, since diffusivity has the dimension of a square length divided by time (L2T-1), the typical duration to reach the final state in equilibrium is necessarily in the order of L2/D . If L ≈ 10 cm , this duration is about one hour. For this duration to be in the order of a second, the enclosure in Figure 4 would have to be about a millimeter long, as would be the case with a small bubble.
4. The turbulent diffusion
In most of the fluid environments in our environment, including air and water, turbulence is almost omnipresent. It is a phenomenon of agitation totally unrelated to the movement of molecules. Within a flow such as the wind, or as a marine current, it manifests itself in the presence of large scale, fairly large and easily measurable speed fluctuations. Even without imposed flow, in the presence of hydrodynamic instability [ 6] , turbulence is present as a set of vortices of all sizes entangled in each other. We can see a certain analogy with the molecular agitation described in the previous sections, but at the vortex scales, much larger than the average free path of the molecules. This analogy led Prandtl [7] to suppose that it was possible to define a mixing length [8] , similar to the average free path of the molecules of a gas.
The concept of mixing length, size noted below , is rather vague but it has the merit of allowing satisfactory orders of magnitude to be established. The situation where it is best justified is that of a boundary layer (see Figure 7). The expression suggested by Prandtl in such a boundary layer and generally adopted is l = κy , where there is the distance to the wall and κ a numerical constant determined by experience. With this expression of the length l , the order of magnitude of the velocity fluctuations at the distance y from the wall can be estimated by u’ ≈ l dU/dy . The analogy with gas agitation suggests reusing the expression of molecular diffusivity (D = cλ/3 ) by replacing c by u’ and λ by l = κy . The turbulent diffusivity Dt within a boundary layer then becomes: Dt ≈ u’l ≈ κ2y2 κ2y2 dU/dy .
For example, let us place ourselves within the atmospheric boundary layer, whose thickness is about a few hundred meters, at a distance from the ground y ≈ 10 m where the average speed is about 10 m.s-1 and where dU/dy ≈ 1 s-1. By adopting the value 0.1 for the constant κ , derived from experiments, these estimates lead to a turbulent diffusivity Dt ≈ 10 m2 .s-1, i. e. one million times higher than the molecular diffusivity. This value reduces the time required to achieve the turbulent mixture to about one-tenth of a second : t ≈ l2/Dt ≈ 0.1 s. But this mixing is not complete because the components are only dispersed to the scale of the smallest vortices, which depends on the viscosity of the fluid. In the case of the atmospheric boundary layer, it is about one millimeter. It is the molecular agitation that completes the mixture to the molecular dimensions , and we know that this requires an L2/D duration. In reality, molecular scattering begins within millimetre eddies where it coexists with turbulent dispersion. To simplify, let us assume that molecular scattering acts alone below the millimeter. With L ≈ 10-3 m and D ≈ 10-5 m2 . s-1, we still obtain a duration of about one tenth of a second .
From these estimates, it can be concluded that:
5. Mass and thermal diffusion
It is by the expression mass diffusivity that we usually refer to the diffusivity of a chemical species contained in the fluid medium. Suppose, therefore, that some of the molecules of the fluid considered, gas or liquid, are different from the others. Let’s take the example of water molecules (H20) in the form of steam, in absolutely calm air over a large liquid area, such as a peaceful lake. And let us now note C the volumetric concentration of water in the air at any altitude z, a quantity initially noted as G before its nature was specified. To evaluate the net flow of water vapour to high altitudes, the law seen above leads to the expression φ = -D dC/dz . It’s Fick’s law . It is essential to be able to calculate the quantity of water extracted by diffusion from low altitudes, but it must be supplemented by a mass balance and by initial and boundary conditions.
Thermal diffusivity expression is reserved for heat transport by molecular agitation. Let us now assume that quantity G is the internal energy E per unit volume of the gas, any infinitesimal variation of which is manifested by a temperature variation dT , according to the law dE = ρCv dT , where Cv denotes the constant volume calorific capacity of the gas. Then the diffusion transport of this internal energy, i. e. heat, becomes φ = -ρCvD dT/dz . It is common to write this expression called Fourier’s Law in one of the following two forms: φ = -k dT/dz , where k = ρCvD = Cv nmcλ/3 is called the thermal conductivity of gas, or φ = -α ρCp dT/dz , where α = k/ρCp is the thermal diffusivity of gas. The quantity Cp then refers to the heating capacity at constant gas pressure.
The physical properties of the gases, especially air, introduced above (D, k, α, μ, ν ) are related to the molecular parameters n, m, c and λ . Among them, for a given density gas, only the velocity of molecules c is likely to vary with temperature T . And we saw that this dependence could be written: T = Mc2/3R = mc2/3kB . It can be deduced that the diffusivities of a gas (D, k, α, μ, ν ) vary like the square root of its temperature .
6. Diffusion of movement: viscosity
Let us now assume that the above notions remain valid in a fluid set in motion at macroscopic scales by moving a wall in its own plane. This hypothesis is very well justified as long as the typical durations of macroscopic motion (seconds or minutes, in general) are considerably longer than the time between two collisions of a molecule (about 10-11 s).

The above reasoning also applies when, instead of being materialized by a wall, the plane z = 0 is an interface between two fluid layers, one of which is moving in its own plane, at the velocity u , between the fluid above it and the fluid below. Newton’s law thus makes it possible to express the tangential force, often called friction , that the fluid layers exert on each other. This tangential force, oriented in the velocity direction, is added to the pressure force, which is oriented according to normal at the interface (Read Pressure, Temperature and Heat ).
7. The mechanism of diffusion in liquids
The fact that all liquids have their own volume implies that the molecules that compose them are close to each other. The average distance between neighbouring molecules depends on the pressure exerted on this liquid; under normal conditions (p ≈ 103 hPa) it is slightly larger than the size of the molecules, typically 10-10 to 10-9 m. The thermal agitation of all these molecules, which can be compared to a vibration, gives this liquid medium a certain diffusivity, but this is much lower than that of gases. The difference is essentially due to the fact that, in a liquid, the radius of action of a molecule is less than its size, whereas in a gas, it is the average free path, about 25 times the size of the molecules. This weakness explains why, in order to dissolve the sugar in a cup of coffee, it is necessary to add a macroscopic stirring by stirring the whole with a spoon.
Any particle with a difference from the molecules and present in this medium is constantly subjected to the vibrations of the whole. A balance similar to that for gases in section 3 necessarily shows a net flow of these particles from the richest to the poorest side. This flow rate can still be written with Fick’s law: φ = -D dC/dx , where D denotes the diffusivity of the particles in the liquid and C their volume concentration.
To predict the mass diffusivity of a liquid, which reflects its ability to transport another material species, we have the following law proposed by Einstein in 1905 [11] : D = kBT/6πμr , where kB = 1.38×10-23 J.K-1 , is the Boltzmann constant, T the absolute temperature, μ the dynamic viscosity of the liquid and r the radius of the transported particle. With r ≈ 10-9 m, in a liquid such as water or μ ≈ 10-3 Pa.s, at an ambient temperature close to 300 K, we obtain D ≈ 2×10-10 m2 .s-1, a value about 10 000 times lower than the diffusivity of a gas. In Einstein’s formula, we will notice that T intervenes at the numerator, which reflects the fact that thermal agitation is the real driving force behind diffusion. And the fact that μ and r are involved in the denominator means that viscosity is opposed to diffusion and that the larger the particles, the more difficult it is to diffuse.
For water and for any electrically insulating liquid, heat and mass have similar diffusivities. On the other hand, for liquid metals, electronic conduction is another heat transport mechanism that can be much more important than mass diffusivity. The most well-known example is liquid sodium, used to cool nuclear reactors of the superregenerator type such as Phoenix, which operated at Marcoule from 1973 to 2010. Its thermal diffusivity at a temperature of about 300 K is about 7×10-5 m2 .s-1, more than 10,000 times higher than its mass diffusivity.
8. Messages to remember
References and notes
Cover image. Before sunrise, in the countryside, in the still motionless air, it is by diffusion that contaminants released by vegetation are transported into the air. [Source: pixabay, royalty-free].
[1] A nanometre is one billionth of a metre ( 10-9 m), a micrometre, or micron, is one millionth of a metre (1 μm = 10-6 m).
[2] Ludwig Boltzmann (1844-1906), an Austrian physicist and philosopher, introduced this molecular model called “hard spheres” that leads to a famous equation bearing his name.
[3] It is often substituted by the kinematic viscosity ν, which is the quotient between the viscosity μ and the density ρ, i.e. ν = μ/ρ.
[4] All these velocities, with their respective orientations and values, can be represented using Maxwell’s distribution function. Taking them into account would lead to lengthy calculations beyond the scope of this article.
[5] This expression is better known as kBT = mc2/3 , by introducing the Boltzmann constant kB , related to R and the Avogadro number NA = 6.0248 × 1023 , per kB = R/NA= 1.380 × 10-23 J/K (joule by Kelvin).
[6] For example, at dawn, as soon as the sun begins to warm the ground, by diffusion it heats the lowest layers of air, which become lighter than those above them. This situation where the heavy fluid is located above the light fluid is unstable.
[7] Ludwig Prandtl (1875-1953) was a German physicist, professor at the University of Munich, who made important contributions to fluid mechanics. He is credited with the founding ideas of boundary layer theory, the concept of mixture length and a simple theory for calculating the lift of a finite wing span.
[8] M. Lesieur, Turbulence, EDP Sciences, Grenoble sciences collection, 2013, p. 128.
[9] The property that φ = -τ can be established by writing the global equilibrium of a small gas domain located on the z>0 side of the wall that exerts the tangential force on the fluid -τ. The expression of this global equilibrium is often referred to as the quantity of movement theorem .
[10] The establishment of this expression is actually due to Navier, Fourier’s congener (see the focus on the Fathers of the diffusion concept ).
[11] Albert Einstein , Investigations on the Theory of the Brownian Movement , Dover Publications, Inc. (1985), (ISBN 0-486-60304-0). Reissue of Einstein’s original articles on Brownian motion theory
环境百科全书由环境和能源百科全书协会出版 ( www.a3e.fr ),该协会与格勒诺布尔阿尔卑斯大学和格勒诺布尔INP有合同关系,并由法国科学院赞助。
引用这篇文章: MOREAU René (2019年2月5日), Diffusion, the ultimate step in a good mixture, 环境百科全书,咨询于 2024年9月13日 [在线ISSN 2555-0950]网址: https://www.encyclopedie-environnement.org/en/physics/diffusion-ultimate-step-good-mixture/ .
环境百科全书中的文章是根据知识共享BY-NC-SA许可条款提供的,该许可授权复制的条件是:引用来源,不作商业使用,共享相同的初始条件,并且在每次重复使用或分发时复制知识共享BY-NC-SA许可声明。
文章目录
- 1. The air at rest: an agitated set of molecules
- 2. Molecular parameters with macroscopic properties of a gas, or the reverse
- 3. The mechanism of diffusion in gases
- 4. The turbulent diffusion
- 5. Mass and thermal diffusion
- 6. Diffusion of movement: viscosity
- 7. The mechanism of diffusion in liquids
- 8. Messages to remember
|
|
踢足球的鼠标 · TiN0.3/AlN复合烧结界面扩散现象 2 月前 |
|
|
踢足球的鼠标 · Si中掺杂原子的瞬间增强扩散现象及抑制方法 2 月前 |
|
|
踢足球的鼠标 · 通过拉曼光谱对扩散现象表征- HORIBA 2 月前 |