对称性：场论中诺特定理推导

一、诺特定理简介

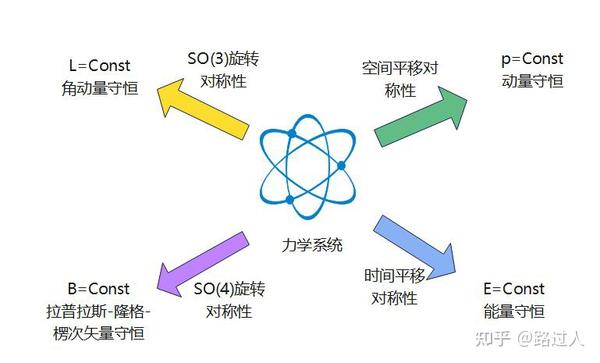
诺特定理是指，对于力学系统的某种对称性，都存在一个守恒量与其对应。

在分析力学中，这常常体现在拉格朗日函数的循环坐标中。当拉格朗日函数不显含某个坐标时，常常对应于一种对称性，这就说明可以寻找到一个守恒量简化力学问题。

二、经典场论的拉格朗日方程

在分析力学中，我们可以了解到，质点的拉格朗日方程可以写作：

\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})-\frac{\partial L}{\partial x}=0

在场论中具有相似的形式。场是具有无穷自由度的质点系，广义坐标被标量场 \phi(x,t) 代替，而原来的x只是指在位置x处的场点，变成了标量场的一个参量，那么新的拉格朗日函数我们可以写出：

L(\phi(x,t),\partial_{\mu}\phi(x,t))~~~\mu=0,1,2,3

也可以写成：

L(\phi,\partial_{\mu}\phi)=\int {d^3x\mathscr{L}(\phi,\partial_{\mu}\phi)}

在闵可夫斯基时空中，0表示t时间,1,2,3分别是空间的三个方向，花写的L是拉格朗日量密度。它是个洛伦兹变换不变量。

因此，最小作用量可以写作：

S=\int{dtL(\phi,\partial_{\mu}\phi)}=\int{dx^4\mathscr{L}(\phi,\partial_{\mu}\phi)}

它的变分为0：

\delta S=\int{dx^4(\frac{\partial \mathscr{L}}{\partial \phi}\delta \phi+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\delta (\partial_{\mu}\phi))}=0

接下来推导思路和质点力学一样了。变分号可以和偏导交换：

\delta S=\int{dx^4(\frac{\partial \mathscr{L}}{\partial \phi}\delta \phi+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)} \partial_{\mu}(\delta\phi))}=0

再利用分部积分法：

\delta S=\int{dx^4[\frac{\partial \mathscr{L}}{\partial \phi}\delta \phi+\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)} \delta\phi)-\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)})\delta\phi]}=0

即：

\delta S=\int{dx^4[\frac{\partial \mathscr{L}}{\partial \phi}-\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)})]\delta\phi}+\int{dx^4\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)} \delta\phi)}=0

注意到第二项是对整个闵可夫斯基空间积分，化为高斯积分后这项为0，所以最小作用量的变分只剩下第一项。由于 \delta \phi 具有任意性，所以只有前面的系数为0才能满足方程。由此我们得到了场论中的拉格朗日方程：

\frac{\partial \mathscr{L}}{\partial \phi}-\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)})=0

三、诺特定理的推导

基于拉格朗日函数，我们开始推导诺特定理。

1.最小作用量变分为0

对于拉格朗日量密度 \mathscr{L}(\phi(x),\partial_{\mu}\phi(x)) ，假设有一个平移操作 x^{\mu}\rightarrow x^{'\mu}=x^{\mu}+\delta x^{\mu} ，相应的场变为 \phi(x^{\mu})\rightarrow \phi^{'}(x^{'\mu})=\phi(x^{\mu})+\delta \phi(x^{\mu}) ，由于具有对称性，新的拉格朗日量密度的最小作用量的变分仍应当为0。

\delta S^{'}=\int{dx^{'4} \mathscr{L}^{'}(\phi^{'}(x^{'}),\partial_{\mu}\phi^{'}(x^{'}))}=0

所以：

\delta S^{'}-\delta S=\int{dx^{'4}\mathscr{L}^{'}}-\int dx^4\mathscr{L}=0

2.对带撇项的处理

我们再将这个式子变形。左边第一项的新坐标的微元，可以用雅可比行列式变换：

dx^{'4}=Jdx^4=|\frac{\partial x^{'\mu}}{\partial x^{\nu}}|dx^4=(\delta_{\nu}^{\mu}+\partial_{\nu}\delta x^{\mu})dx^4

注意到这个平移变换是个无穷小的变换，所以雅可比行列式的对角线上的元素会比非对角大很多，所以我们保留对角线元素：

dx^{'4}=(\delta_{\nu}^{\mu}+\partial_{\nu}\delta x^{\mu})dx^4\approx (1+\partial_{\mu}\delta x^{\mu})dx^4

而左边第一项的新的拉格朗日量密度可以写作：

\mathscr{L}^{'}=\mathscr{L}+\delta \mathscr{L}

所以：

\delta S^{'}-\delta S=\int{dx^4(1+\partial_{\mu}\delta x^{\mu})(\mathscr{L}+\delta \mathscr{L})}-\int dx^4\mathscr{L}=0

忽略二阶变分项，得：

\int{dx^4(\mathscr{L}\partial_{\mu}\delta x^{\mu}+\delta \mathscr{L})}=0

3.对拉氏密度的变分的处理

注意到：

\delta \mathscr{L}=\mathscr{L}^{'}(x^{'})-\mathscr{L}(x)

这个拉氏密度的变分不在同一场点，不能直接做展开。将变分写为：

\delta \mathscr{L}=\mathscr{L}^{'}(x^{'})-\mathscr{L}^{'}(x)+\mathscr{L}^{'}(x)-\mathscr{L}(x)

前两项之差是函数形式不变，场点位置发生变化，可以做泰勒展开：

\mathscr{L}^{'}(x^{'})-\mathscr{L}^{'}(x)\approx\partial_{\mu}\mathscr{L}^{'}(x)\delta x^{\mu}\approx \partial_{\mu}\mathscr{L}(x) \delta x^{\mu}

（第一个约等于号忽略了 O((\delta x^{\mu})^2) 及以上的项；第二个约等于号用到了场的连续性，很近的两个场点拉氏密度近似相等。)

而对于变分的第三项和第四项，是场点不动，拉氏密度在变化，我们记这样的变分为 \overline{\delta} ，从而可以写成：

\overline{\delta}\mathscr{L}=\mathscr{L}^{'}(x)-\mathscr{L}(x)=\frac{\partial \mathscr{L}}{\partial \phi}\overline{\delta }\phi+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}(\partial_{\mu}\phi)

综上我们可以得到：

\delta \mathscr{L}=\partial_{\mu}\mathscr{L}(x) \delta x^{\mu}+\frac{\partial \mathscr{L}}{\partial \phi}\overline{\delta} \phi+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}(\partial_{\mu}\phi)

顺带得到带横线的变分和不带横线变分的关系：

\delta \mathscr{L}=\overline{\delta}\mathscr{L}+\partial_{\rho}\mathscr{L}(x) \delta x^{\rho}

4.综合处理

将第3小点的倒数第二个式子的式子代入到第2小点最后的式子中：

\int{dx^4(\mathscr{L}\partial_{\mu}\delta x^{\mu}+\partial_{\mu}\mathscr{L}(x) \delta x^{\mu}+\frac{\partial \mathscr{L}}{\partial \phi}\overline{\delta} \phi+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}(\partial_{\mu}\phi))}=0

将前两项合并为全微分，后两项按照拉格朗日方程推导过程的套路，得到：

\int{dx^4\{(\partial_{\mu}(\mathscr{L}(x)\delta x^{\mu})+[\frac{\partial \mathscr{L}}{\partial \phi}-\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)})]\overline{\delta}\phi +\partial_{\mu}[\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}\phi]}\}=0

注意到拉格朗日方程满足：

\frac{\partial \mathscr{L}}{\partial \phi}-\partial_{\mu}(\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)})=0

所以方程化为：

\int{dx^4\{\partial_{\mu}(\mathscr{L}(x)\delta x^{\mu})+\partial_{\mu}[\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}\phi]}\}=0

把偏导合并：

\int{dx^4\partial_{\mu}(\mathscr{L}(x)\delta x^{\mu}+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\overline{\delta}\phi})=0

将上式化成统一变分形式。利用第3点最后一个公式，并利用度规关系：

\int{dx^4\partial_{\mu}(\mathscr{L}(x)g_{\rho}^{\mu}\delta x^{\rho}+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\delta\phi}-\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\partial_{\mu}\phi\delta x^{\rho})=0

这里面有两个变分形式，一个是 \delta x^{\rho} ，一个是 \delta\phi 。如果能有一套参量 \beta 描述它们，那么：

\int{dx^4\partial_{\mu}[(\mathscr{L}(x)g_{\rho}^{\mu}-\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\partial_{\mu}\phi)\frac{\delta x^{\rho}}{\delta\beta}+\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\frac{\delta\phi}{\delta\beta}}]\delta\beta=0

5.守恒量寻找

我们先将第4小点的中括号里的东西定义为流密度（定义负号为了使能动量不小于0）：

j^{\mu}=-(\mathscr{L}(x)g_{\rho}^{\mu}-\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\partial_{\mu}\phi)\frac{\delta x^{\rho}}{\delta\beta}-\frac{\partial \mathscr{L}}{\partial (\partial_{\mu}\phi)}\frac{\delta\phi}{\delta\beta}

那么：

\int{dx^4\partial_{\mu}j^{\mu}}=0

因此我们可以知道，流密度的四维散度为0，从而可知四维的流密度是守恒的。

除了流外，还可以找到守恒荷。

\int{dx^4\partial_{\mu}j^{\mu}}=\int{dx^0\partial_0(\int{dx^3j^0)}}+\int{dx^0\int{dx^3\partial_{\mu}j^{\mu}}}=0

注意到第二项又是对全空间积分，积分值为0，从而发现只剩下第一项。

但第一项正是对时间的偏导数为0，所以偏导里面的东西就是守恒荷了：

\int_{\Omega}{dx^3j^{0}}=Q=Const

其中 \Omega 表示的是三维的全空间

四、总结

综上来看，我们从拉格朗日函数具有的对称性出发，利用最小作用量变分值不变的条件，导出了守恒流的形式和守恒荷的形式，证明了对于力学系统存在的某种对称性，一定存在守恒量与其对应。诺特定理证毕。

五、参考文献

[1]黄涛编著.量子场论导论[M].