在塑性理论学习过程中,经常见到一些概念“ Yielding, Mises stress,Hill's potential,backstress ”等,这些概念该怎么去理解呢?我们一起回顾与学习一下塑性相关的概念叭~

1. 屈服准则
1.1 屈服 Yielding
当处于初始平衡状态或未变形状态的物体受到体力或表面力的作用时,物体会发生相应的变形,直至达到新的力学平衡状态或变形状态。内部的体力如重力场,而表面力是通过与其他物体接触施加的力。
外力(用应力表征)和物体变形(用应变表征)之间的关系称为 应力-应变关系 。这些关系代表了构成物体的材料的性质,也被称为 本构方程constitutive equations 。
下图是研究低碳钢梁单轴受拉应变响应时得到的曲线:
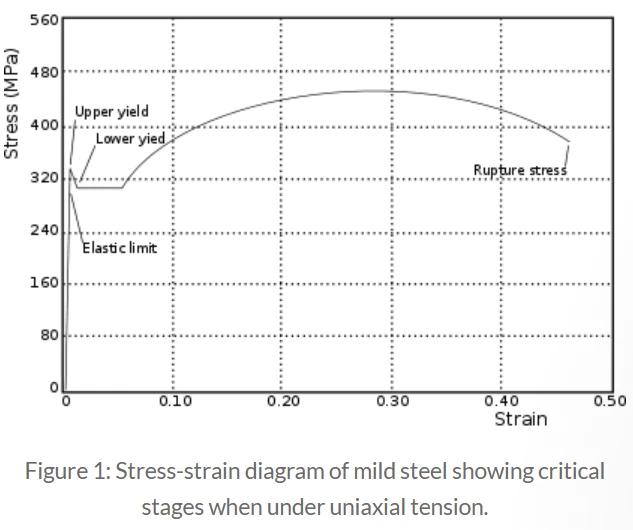
其中:
Elastic Limit 弹性极限: 弹性极限定义了在应力和应变过程中能量不损失的区域。也就是说,不超过弹性极限的过程是可逆的。这个极限也被称为 屈服应力 。超过这个极限,变形不再是弹性的,而开始是塑性的,变形包括了不可逆的部分。这里用Sy表示单轴拉伸弹性极限的应力值。
Upper yield and lower yield 上屈服和下屈服: 当低碳钢处于塑性范围内并达到一个临界点(称为 屈服上限 )时,它将迅速下降到 屈服下限 ,从这个下限开始,在恒定的应力下发生变形,直到它再次开始抵抗变形。
Rupture/fracture stress 断裂应力: 断裂是由应力引起的物体分离。随着材料变得越来越细,施加的压力越来越大,直到它在断裂应力点突然断裂。像低碳钢这样的材料——只有在大的塑性变形后才表现出断裂的特性——被称为 延性材料 。此处所示的断裂称为 延性断裂/延性损伤/韧性断裂 。
通常用下图近似大部分材料:
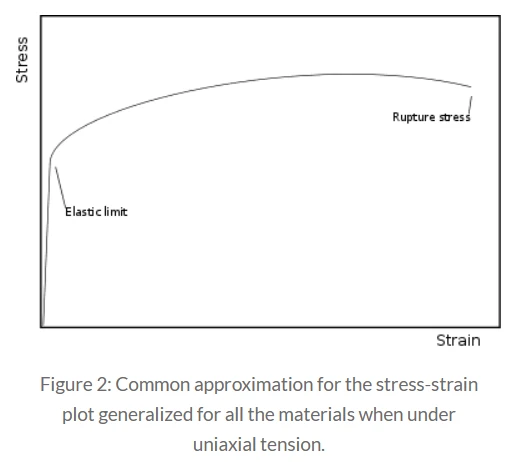
1.2 Von Mises Yield Criterion 冯·米赛斯屈服准则
Mises Stress: 冯米塞斯应力是用来确定给定材料是否会屈服或断裂的一个值。 它主要用于韧性材料,如金属。von Mises屈服准则指出,如果材料在载荷作用下的von Mises应力等于或大于同一材料在简单拉伸作用下的屈服极限,则材料将屈服。
冯米塞斯应力是一种广泛应用于金属和其他延性材料的屈服判据。如果作用在物体上的应力分量大于这个阈值,材料就会屈服。
若τ为应力张量,Mises应力用 τv表示,则定义为:
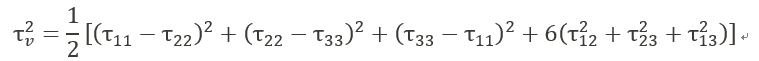
因此,von Mises屈服准则通常也被改写为:
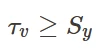
如果von Mises应力大于简单拉伸屈服极限应力,则材料发生屈服。
Mises应力用主应力表示为:
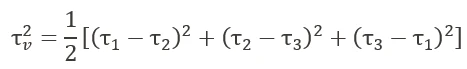
例如,von Mises应力可以应用于油气储层钻井等领域,在这些领域中,管道预计将处于高压和复合载荷条件下。在这种情况下,von Mises应力公式可以写成:
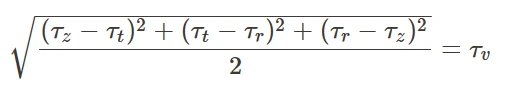
其中z、r、t分别为轴向、径向和切向应力。
冯·米塞斯应力不是真正的应力。它是一个理论值,允许将一般三维应力与单轴应力屈服极限进行比较。Von Mises应力等于或大于材料的简单拉屈服应力,则将发生屈服。
1.3 Tresca Yield Criterion Tresca屈服准则
Tresca屈服准则 是用于确定材料屈服前最大应力的通用准则的另一个例子。与von Mises方法相比,用Tresca方法计算屈服总是得到较低的结果。在科学界,它通常被认为是一种更为保守的失效估计,也称为 最大剪应力屈服准则 。
最大剪应力的最一般表达式为:
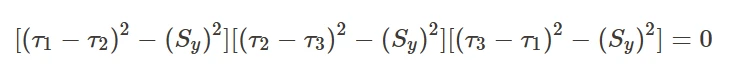
根据应力分量的大小顺序(τ1>τ2>τ3)有助于简化这一准则。上面的表达式简化为:
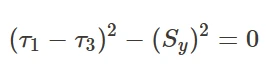
treca屈服准则是分段线性的,而von Mises屈服准则是非线性的。然而,Tresca屈服面可能包含奇异点。两种情况的预测差异相对较小。
1.4 Hill's potential Hill屈服准则
Mises屈服准则和Tresca屈服准则适用于描述各向同性的金属材料,而对于 各向异性 的金属材料采用Hill屈服准则描述;
Hill势函数是Mises函数的简单扩展,它可以用直角笛卡尔应力分量表示为:
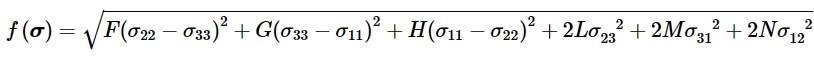
式中,F、G、H、L、M、N为材料在不同方向上试验得到的常数。定义为:
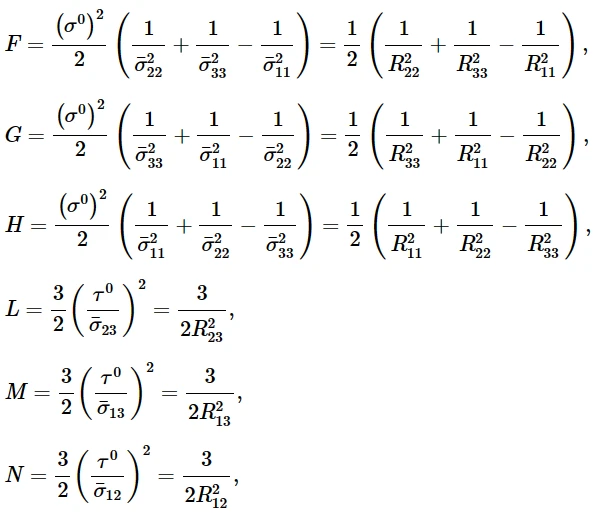
其中:
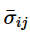
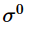
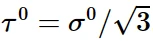
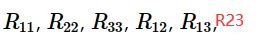
因此,以上六个屈服应力比的定义如下:
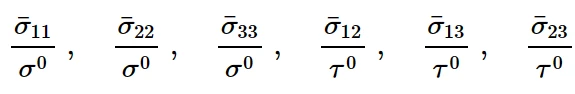
当Hill势函数=0时为屈服面,小于0为弹性阶段,大于0将发生屈服。
2. 经典的金属塑性应力应变曲线分析
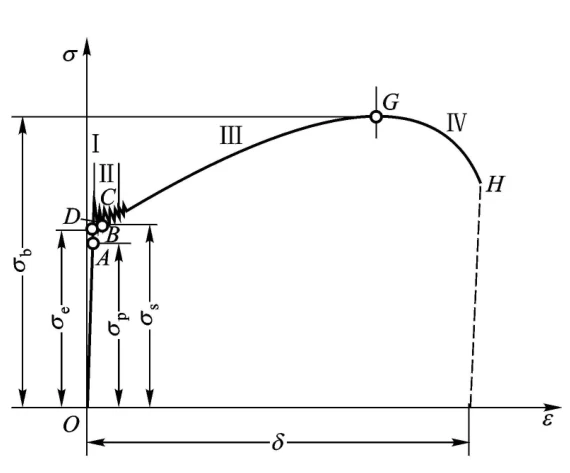
可以分为4个阶段:

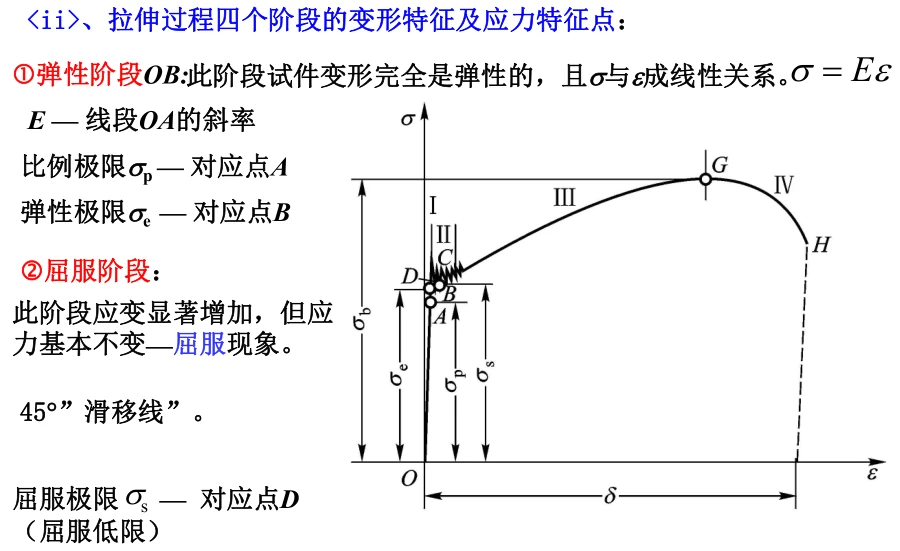
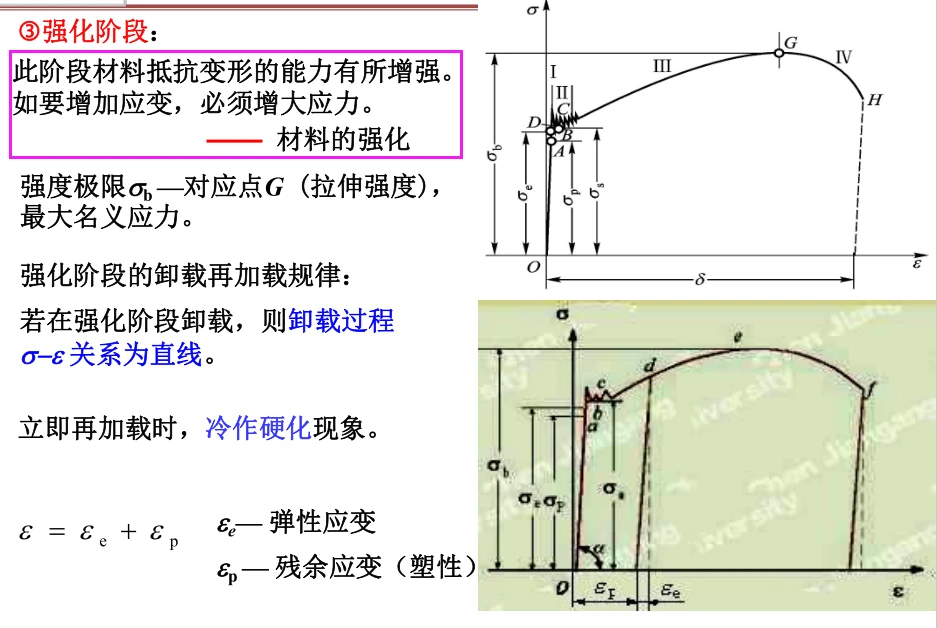
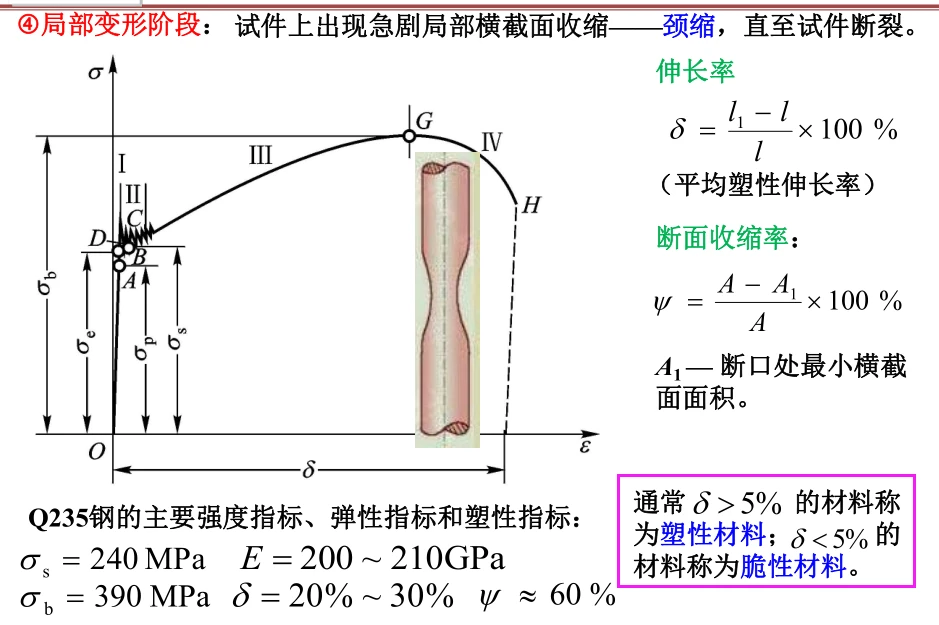
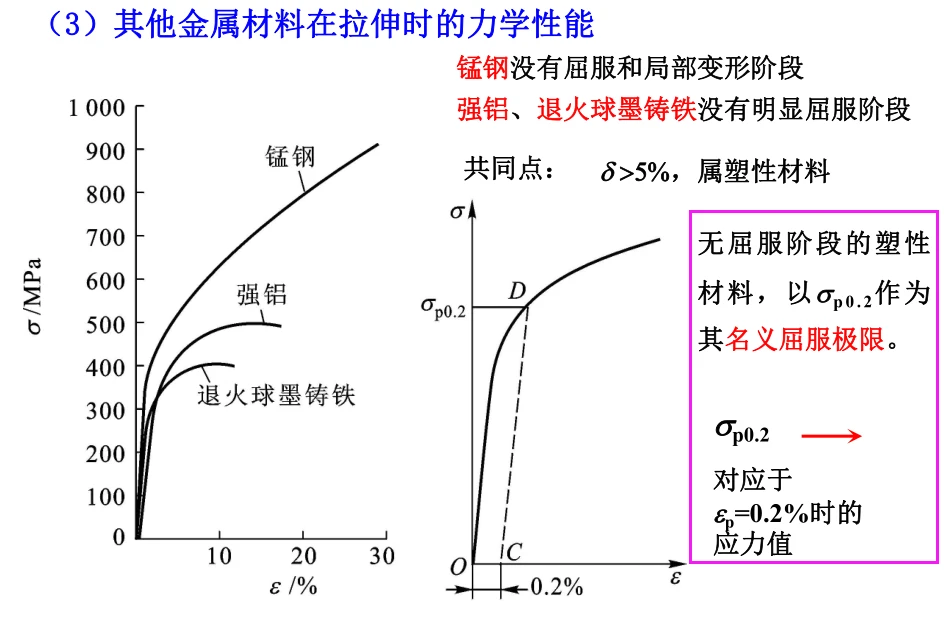
3. 简化的塑性模型



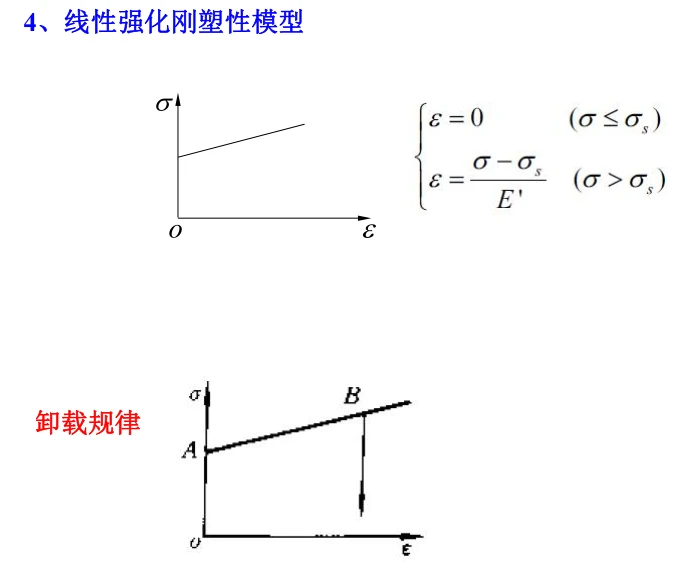

4. 强化准则/硬化准则
由上述第三节简化的弹塑性模型可知,理想的塑性材料在屈服点之后的斜率为0,然鹅现实中的材料在屈服点之后往往斜率不为0,具有 应变强化 效应,也称为 应变硬化 。常见的强化准则有两类: 等向强化 和 随动强化
4.1 等向强化
等向强化(Isotropic Hardening):也叫各向同性硬化,“等向”指 屈服面向各个方向均匀的扩张。卸载后的压缩屈服极限等于在拉伸阶段得到的最大应力 。一般用于大应变或单向屈服加载的计算中,不适用于交变载荷(因为无法模拟包辛格效应)。
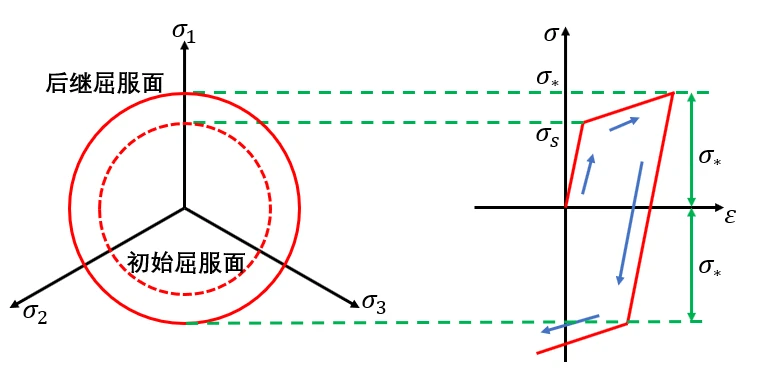
4.2 随动强化
随动强化(Kinematic Hardening):
屈服面的面积不变,中心向屈服方向移动
。
α 表示屈服面中心的坐标,也被称之为
背应力
backstress
;
大多数受小应变交变载荷的金属遵循随动强化。随动强化满足
包辛格效应
,即屈服面变化后,若拉伸屈服极限增加时,压缩屈服极限减小,但两个屈服极限之间的差2σs保持不变。
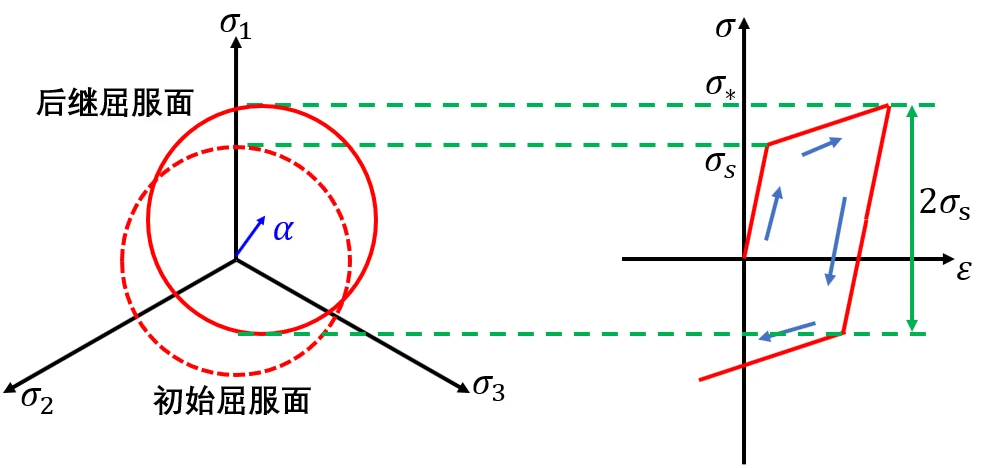
随动硬化模型描述 各向异性,且不适用于循环的大应变载荷;
随动硬化模型常见的有Prager 模型和 Ziegler模型:Prager认为在塑性流动过程中屈服面沿着塑性应变率的方向移动并且保持初始的形状和大小不变,而Ziegler认为屈服面应该沿着𝜎-α的方向平移:
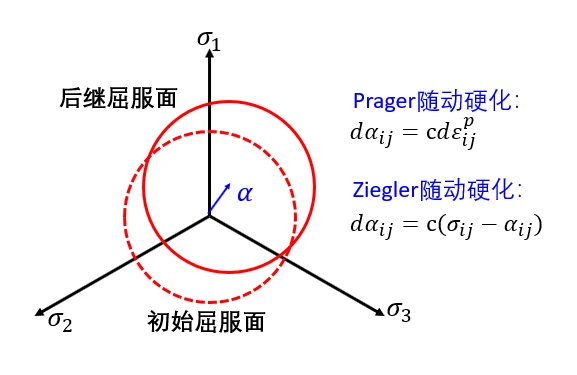
4.3 混合硬化
混合硬化可以理解为各向同性硬化与随动硬化的叠加,屈服面在空间中不仅发生膨胀或收缩,同时产生平移:
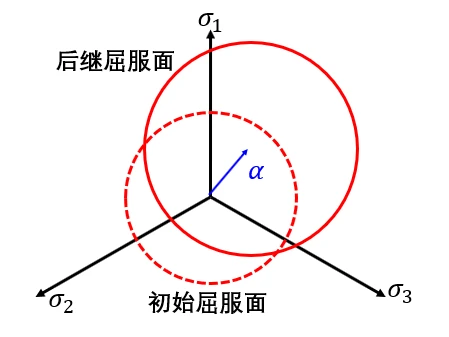
需要注意的是: 以上各屈服面均为圆形,这是因为使用的Mises屈服应力,Mises屈服应力在3维主应力上为一个圆形,对应的Tresca屈服应力为正六边形;
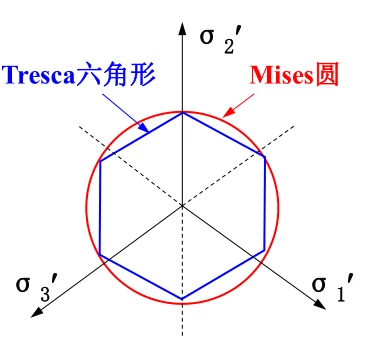
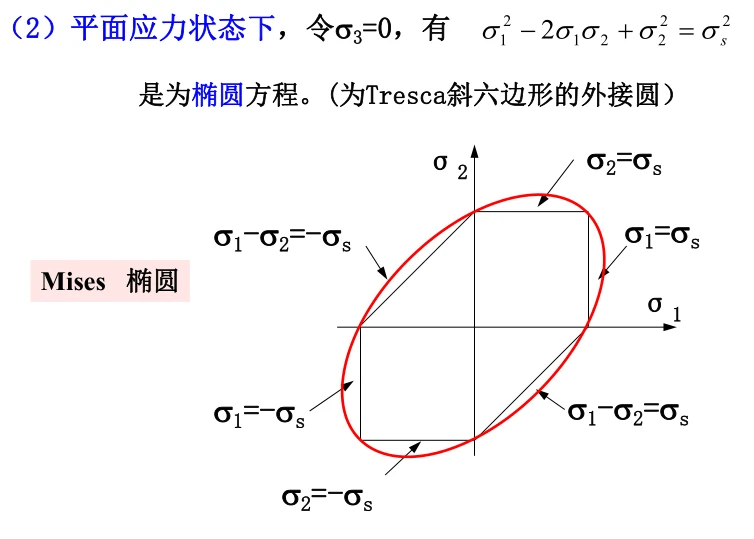
在平面应力状态下:

5. 流动准则
流动准则描述了发生 屈服时塑性应变的方向 。分为关联流动与非关联流动。
关联流动 : 塑性应变垂直于屈服面的流动准则。适用于金属和其它呈现不可压缩的非弹性材料;
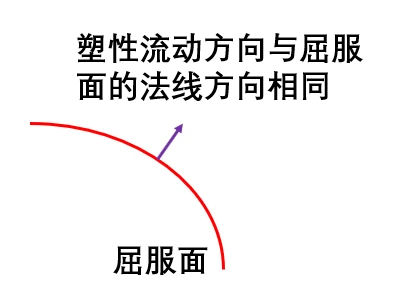
非关联流动 :塑性应变不垂直于屈服面的流动准则。适用于颗粒材料(摩擦材料),例如 Drucker-Prager本构模型中剪胀角与内摩擦角不同;

6. 滞回环
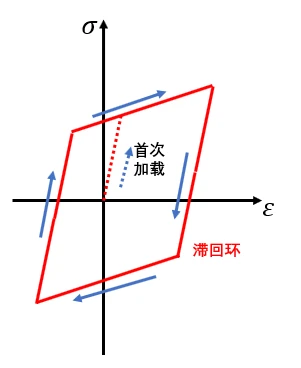
当金属材料处于 周期性双向屈服载荷 下,由于随动强化准则的作用,应力应变曲线会出现塑形滞回环,滞后环所包围的面积即为 循环韧性 ,这部分的应变能将以热量的形式释放,如反复弯曲的铁丝会发热。

说明:本系列文章是up主边学边整理的,可以看作是学习笔记,存在的错误欢迎指出。
如果对你有帮助,请一键三连吧~关注up主,学习不迷路~
欢迎评论区交流讨论~