什么是Black-Scholes期权定价模型？

Black-Scholes模型可以说是最经典的用来做期权定价和对冲的数学模型，它由Black和Scholes首先提出，用来定价欧式期权（European option），后经Merton修改，使其在有股息（dividend）的情况下也可使用。此模型假设期权的基础股票（underlying stock）遵循几何布朗运动（geometric Brownian motion），并依此给出期权的唯一价格。此外，它还被用于推导期权的Greeks，以构造对冲（hedge）资产组合来消除风险。在本篇文章中，我们来介绍Black-Scholes模型和与资产定价相关的结论。

1 Black-Scholes偏微分方程和Black-Scholes公式

我们首先介绍Black-Scholes偏微分方程（PDE），即期权价格满足的一个偏微分方程。我们来考虑一个成交价格（strike price）为 K 、到期时间（maturity）为 T 、无股息支付的欧式看涨期权（European call option）。假设基础股票的价格 S_t 满足几何布朗运动

dS_t=\mu S_tdt+\sigma S_tdW_t\\

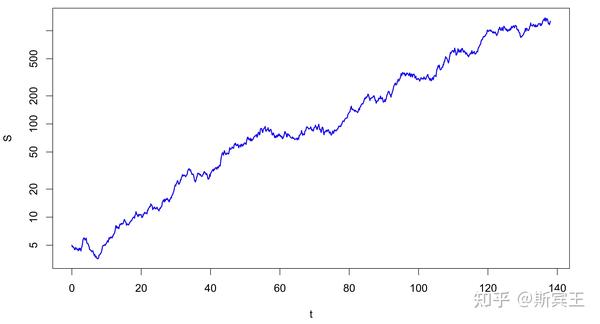
其中 W_t 是标准布朗运动（standard Brownian motion）。令在时间 0 时有 1 元钱现金账户（cash account）在时间 t 的价值为 \exp(rt) 元，其中 r 是恒定利率（constant interest rate），即 dB_t=rB_tdt 。将看涨期权在时间 t 的价格写作 C(S,t) ，根据伊藤引理，我们有

dC(S,t)=(\frac{\partial C}{\partial t}+\mu S_t\frac{\partial C}{\partial S}+\frac{1}{2}\sigma^2S_t^2\frac{\partial^2 C}{\partial S^2})dt+\sigma S_t\frac{\partial C}{\partial S}dW_t\\

现在构造自融资（self-financing）投资组合（没有外部金钱流入或流出） \Pi_t ，在时间 t 时，持有 x_t 单位的现金账户和 y_t 单位的股票，所以 \Pi_t=x_tB_t+y_tS_t 。我们选取 x_t 和 y_t 的值，以复制看涨期权的价值。根据自融资假设，

d\Pi_t=x_tdB_t+y_tdS_t\\ =(rx_tB_t+\mu y_tS_t)dt+\sigma y_tS_tdW_t\\

当我们把前面两个等式的相应项对应起来，我们有 y_t=\frac{\partial C}{\partial S} 和 rx_tB_t=\frac{\partial C}{\partial t}+\frac{1}{2}\sigma^2S_t^2\frac{\partial^2 C}{\partial S^2} 。若我们设置 V_0=C_0 为自融资投资组合的起始价值，我们有 V_t=C_t\ \forall\ t 。将前面两个等式带入 C_t=x_tB_t+y_tS_t ，我们得到

\frac{\partial C}{\partial t}+rS_t\frac{\partial C}{\partial S}+\frac{1}{2}\sigma^2S_t^2\frac{\partial^2 C}{\partial S^2}=rC\\

通过变量变换可以将Black-Scholes PDE \frac{\partial C}{\partial t}+rS\frac{\partial C}{\partial S}+\frac{1}{2}\sigma^2S^2\frac{\partial^2 C}{\partial S^2}-rC=0 转化为热方程（heat equation） \frac{\partial u}{\partial \tau}=\frac{1}{2}\sigma^2\frac{\partial^2 u}{\partial x^2} ，其中 \tau=T-t ， u=Ce^{r\tau} ， x=\ln S+(r-\frac{1}{2}\sigma)\tau 。由于边界条件（boundary condition）为 u(x,0)=u_0(x) 的热方程的解是 u(x,\tau)=\frac{1}{\sqrt{2\pi\tau}\sigma}\int_{-\infty}^\infty u_0(z)\exp(-\frac{(x-z)^2}{2\sigma^2\tau})\ dz ，且欧式看涨期权的边界条件为 u_0(S_T,K)=\max(S_t-K,0) ，我们可以得到 u(S,\tau)=\frac{1}{\sqrt{2\pi\tau}\sigma}\int_{\ln K}^\infty(e^z-K)\exp(-\frac{(x-z)^2}{2\sigma^2\tau})\ dz 。令 \epsilon=\frac{z-x}{\sigma\sqrt{\tau}} ，当 z=\ln K 时， \epsilon=\frac{\ln(K/S)-(r-\sigma^2/2)\tau}{\sigma\sqrt{\tau}}=-d_2 ，所以

u(S,\tau)=\int_{-d_2}^\infty(Se^{(r-\sigma^2/2)\tau+\sigma\sqrt{\tau}\epsilon}-K)\frac{1}{\sqrt{2\pi}}\exp(-\epsilon^2/2)\ d\epsilon\\

通过计算此积分（在下一部分中进行）和 C=re^{-r\tau} 这一关系，我们可以得到欧式看涨期权定价的Black-Scholes公式

C(S,t)=S_tN(d_1)-e^{-r(T-t)}KN(d_2)\\ d_1=\frac{\ln(S_t/K)+(r+\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}\\ d_2=d_1-\sigma\sqrt{T-t}=\frac{\ln(S_t/K)+(r-\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}\\

这里 N(\cdot) 是标准正态分布（standard normal distribution）的累积分布函数（CDF）。类似地，我们可以得到欧式看跌期权（European put option）定价的Black-Scholes公式

P(S,t)=e^{-r(T-t)}KN(-d_2)-S_tN(-d_1)\\

2 风险中性定价

在上一部分中，我们发现，Black-Scholes PDE中没有出现 \mu ，所以当 \mu=r 时Black-Scholes PDE仍成立。这时投资者对持有股票没有溢价（premium）需求，而这只有在投资者是风险中性（risk-neutral）时才会发生，所以我们可以用风险中性定价求得Black-Scholes模型中欧式看涨期权的价格。

在风险中性概率测度（risk-neutral probability measure）下，股价遵循的几何布朗运动的漂移项（drift term）是无风险利率 r

dS_t=r S_tdt+\sigma S_tdW_t\\

在风险中性概率测度下，期权价格时预期回报（expected payoff）用无风险利率的折现值（discounted value），即 C_t=e^{-r\tau}\mathbb{E}^{\mathrm{rn}}_t[V_T] ，这里 V_T 是期权在到期时间 T 的回报。对 \ln S 应用伊藤引理，我们有 d\ln S=(r-\sigma^2/2)dt+\sigma dW_t ，所以 \ln S_T\sim N(\ln S+(r-\sigma^2/2)\tau,\sigma^2\tau) ，即 S_T=Se^{(r-\sigma^2/2)\tau+\sigma\sqrt{\tau}\epsilon} ，其中 \epsilon\sim N(0,1) 。对于欧式看涨期权， V_T=\max(S_T-K,0) ，且当 Se^{(r-\sigma^2/2)\tau+\sigma\sqrt{\tau}\epsilon}=K 时， \epsilon=\frac{\ln(K/S)-(r-\sigma^2/2)\tau}{\sigma\sqrt{\tau}}=-d_2 。那么，折现预期回报就是上一部分中需要计算的积分

\mathbb{E}^{\mathrm{rn}}_t[\max(S_T-K,0)]=\int_{-d_2}^\infty(Se^{(r-\sigma^2/2)\tau+\sigma\sqrt{\tau}\epsilon}-K)\frac{1}{\sqrt{2\pi}}e^{-\epsilon^2/2}\ d\epsilon\\ =Se^{r\tau}\int_{-d_2}^\infty\frac{1}{\sqrt{2\pi}}e^{-(\epsilon-\sigma\sqrt{\tau})^2/2}\ d\epsilon-K\int_{-d_2}^\infty\frac{1}{\sqrt{2\pi}}e^{-\epsilon^2/2}\ d\epsilon\\

令 \tilde{\epsilon}=\epsilon-\sigma\sqrt{\tau} ，当 \epsilon=-d_2 时， \tilde{\epsilon}=-d_2-\sigma\sqrt{\tau}=-d_1 。这样， Se^{r\tau}\int_{-d_2}^\infty\frac{1}{\sqrt{2\pi}}e^{-(\epsilon-\sigma\sqrt{\tau})^2/2}\ d\epsilon=Se^{r\tau}\int_{-d_1}^\infty\frac{1}{\sqrt{2\pi}}e^{-\tilde{\epsilon}^2/2}\ d\tilde{\epsilon}=Se^{r\tau}(1-N(-d_1))=Se^{r\tau}N(d_1) ，且 K\int_{-d_2}^\infty\frac{1}{\sqrt{2\pi}}e^{-\epsilon^2/2}\ d\epsilon=K(1-N(-d_2))=KN(d_2) 。所以我们得到欧式看涨期权的Black-Scholes公式

C(S,t)=S_tN(d_1)-e^{-r(T-t)}KN(d_2)\\

类似地，我们可以得到欧式看跌期权（European put option）定价的Black-Scholes公式

P(S,t)=e^{-r(T-t)}KN(-d_2)-S_tN(-d_1)\\

当期权的基础股票支付恒定连续股息 q 时，在风险中性概率测度下，

dS_t=(r-q)S_tdt+\sigma S_tdW_t\\

这种情况下的Black-Scholes公式是

C(S,t)=e^{-q(T-t)}S_tN(d_1)-e^{-r(T-t)}KN(d_2)\\ P(S,t)=e^{-r(T-t)}KN(-d_2)-e^{-q(T-t)}S_tN(-d_1)\\ d_1=\frac{\ln(S_t/K)+(r-q+\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}\\ d_2=d_1-\sigma\sqrt{T-t}=\frac{\ln(S_t/K)+(r-q-\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}\\

值得注意的是，Black-Scholes模型是一个完全模型（complete model），即所有衍生品都是可复制的（replicable），且每个衍生品都有唯一定价。

3 波动率曲面

Black-Scholes模型是一个理想化的模型，它在实践中的表现并没有那么好。例如，模型假设股价遵循连续的几何布朗运动，而在现实中股价可能出现跳跃。此外，如果股价波动率如模型所规定那样是恒定的，隐含波动率曲面（implied volatility surface）应该是平的。隐含波动率是当期权的Black-Scholes价格等于其市场价格时，股价波动率的值，它由隐函数

C(S,K,T)=BS(S,T,r,q,K,\sigma(K,T))\\

定义，这里 \sigma 是关于成交价 K 和到期时间 T 的函数，而 C(S,K,T) 代表对应期权的市场价格。

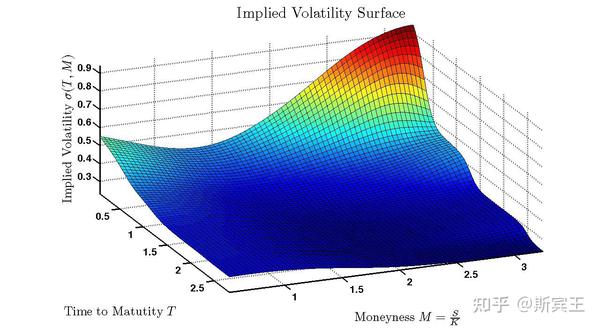
波动率曲面的主要特征之一是，成交价越低的期权，隐含波动率越高。在到期时间固定时，这一特征被称为波动率倾斜（volatility skew）。当成交价固定时，隐含波动率可以随到期时间增长增大或减小。普遍来说，当 T\to\infty ， \sigma(K,T) 会收敛于一个常数。而当 T 较小时，我们会观察到反转波动率曲面（inverted volatility surface），短期期权的隐含波动率远高于期限更长的期权。

无套利原则（no arbitrage principle）对波动率曲面的形状做出了规定。首先，隐含波动率是非负的。此外，给定固定到期时间，波动率倾斜不能太陡，否则会出现蝴蝶套利（butterfly arbitrage）机会。如果套利不存在，那么当 K_1<K_2 ，看跌期权价格必须满足 P(K_1)<P(K_2) 。可是若波动率倾斜太陡，可能会出现 P(K_1)>P(K_2) ，即套利机会。还有，隐含波动率的期限结构（term structure）的反转程度不能太高，否则会出现日历价差套利（calendar spread arbitrage）机会。假设 r=q=0 ，固定成交价 K ，根据风险中性定价，到期时间为 T 的看涨期权在时间 t 的价格是 C_t(T)=\mathbb{E}_t[\max(S_T-K,0)] 。由于 \max(S_T-K,0) 是一个下鞅（submartingale）， C_t(T) 关于 T 单调递增。而如果期限结构的反转程度太高，这可能不成立。

对于波动率倾斜（给定一到期时间，隐含波动率随成交价降低而升高），有两条主要原因。一是投资者的风险厌恶（risk-aversion）心理。首先，股价不遵循几何布朗运动，而是存在跳跃，且向下的跳跃比向上的跳跃更大更频繁。其次，当市场下行，恐惧心理会使波动率增加。还有，投资者对于低成交价期权的需求更大，因为他们会购买价外（out-of-the-money）看跌期权来作为投资组合的保险。第二条主要原因是杠杆效应（leverage effect），即权益（equity）波动率随权益减小而增大。Merton的研究指出，公司的权益可以看作关于公司总价值的看涨期权。由于公司总价值等于其权益加负债（debt），即 V=D+E ，当负债风险较小时， \sigma_V\approx\frac{E}{V}\sigma_E ，即

\sigma_E\approx\frac{V}{E}\sigma_V\\

4 Greeks

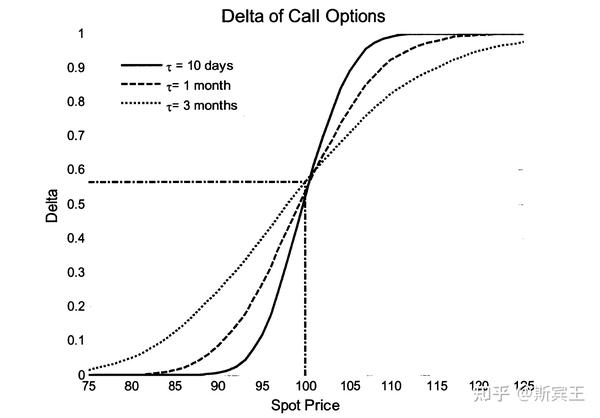
期权的Greeks衡量期权价格关于随参数变化的敏感程度。期权的Delta衡量期权价格关于随股价变化的敏感程度。对于欧式看涨和看跌期权，

\delta_C=\frac{\partial C}{\partial S}=e^{-qT}N(d_1)\\ \delta_P=\frac{\partial P}{\partial S}=-e^{-qT}(1-N(d_1))\\

Delta是最重要的Greek，因为它通常会带来最大的风险。许多投资者会在一天结束时将Delta归零，并遵循Black-Scholes模型定义的Delta中性对冲方法。

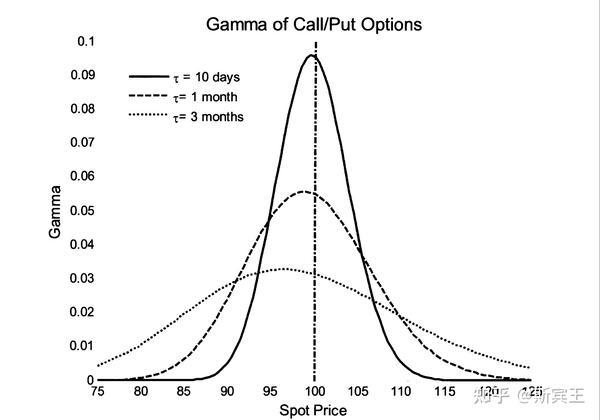
另外投资者还会关注Delta关于随股价变化的敏感程度Gamma。对于欧式看涨和看跌期权，它们的Gamma相等，

\Gamma=\frac{\partial^2 C}{\partial S^2}=e^{-qT}\frac{N'(d_1)}{S\sigma\sqrt{T}}\\

这里 N'(\cdot) 是标准正态分布的概率分布函数（PDF）。Gamma由于期权的凸性（convexity）总是正的。有些投资者会做多Gamma，利用Gamma scalping来挣钱。他们会通过再平衡（rebalance）投资组合来实现Delta中性。

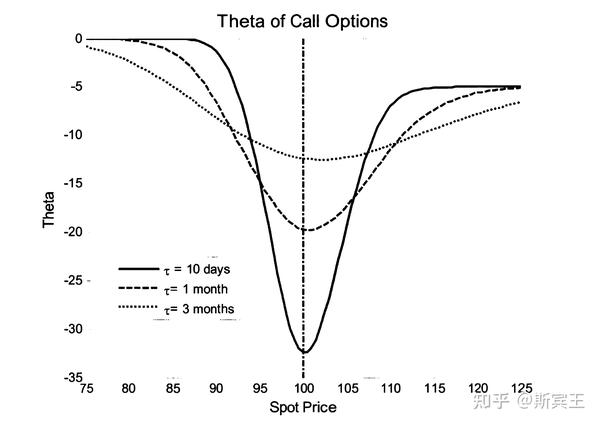
另一个重要的Greek是Theta，它是期权价格关于随到期时间负变化的敏感程度。对于欧式看涨和看跌期权，

\theta_C=-\frac{SN'(d_1)\sigma e^{-qT}}{2\sqrt{T}}+qSe^{-qT}N(d_1)-re^{-qT}N(d_2)\\ \theta_P=-\frac{SN'(d_1)\sigma e^{-qT}}{2\sqrt{T}}-qSe^{-qT}N(-d_1)+re^{-qT}N(-d_2)\\

价内（in-the-money）看跌期权的 \theta 可以是正的，且当 q 较大时，价内看涨期权的 \theta 也可以是正的。然而，在一般情况下，看涨期权和看跌期权的 \theta 都为负值。

我们可以根据Black-Scholes PDE推出Delta、Gamma和Theta的关系。由于

\frac{\partial V}{\partial t}+(r-q)S\frac{\partial V}{\partial S}+\frac{1}{2}\sigma^2S^2\frac{\partial^2 V}{\partial S^2}=rV\\

这里 V 指代投资组合的价值，我们可以得到关系

\theta+(r-q)S\delta+\frac{1}{2}\sigma^2S^2\Gamma=rV\\

如果投资组合是Delta对冲组合，即对投资组合连续地再平衡被，以保证 \delta=0 ，那么

\theta+\frac{1}{2}\sigma^2S^2\Gamma=rV\\

不难看出，从Gamma得到的收益会被从Theta产生的损失抵消。

5 奇异期权定价

Black-Scholes模型还可以被应用于奇异期权（exotic option）的定价。根据其回报函数，我们可以轻易得到几种指状期权（digital option）的Black-Scholes价格。若在到期时间现价大于成交价，现金或有看涨期权（cash-or-nothing call option）支付 1 元，否则支付 0 元，它的Black-Scholes价格是

C=e^{-r(T-t)}N(d_2)\\

类似地，现金或有看跌期权的Black-Scholes价格是

P=e^{-r(T-t)}N(-d_2)\\

若在到期时间现价大于成交价，资产或有看涨期权（asset-or-nothing call option）支付 1 单位资产，否则支付 0 元，它的Black-Scholes价格是

C=Se^{-q(T-t)}N(d_1)\\

类似地，资产或有看跌期权的Black-Scholes价格是

P=Se^{-q(T-t)}N(-d_1)\\

事实上，欧式看涨期权可被分解为做多 1 单位的资产或有看涨期权加上做空 K 单位的现金或有看涨期权，欧式看跌期权可被分解为做多 K 单位的现金或有看跌期权加上做空 1 单位的资产或有看跌期权。

另外，指状期权还可以用不依靠特定模型的方式来定价。以现金或有看涨期权为例，它的价格可被定义为

D(K,T)=\lim_{\Delta K\to0}\frac{C(K,T)-C(K+\Delta K,T)}{\Delta K}=-\frac{\partial C(K,T)}{\partial K}\\

这意味着指状期权可以由波动率曲面唯一地定价。令 C(K,T)=C_{BS}(K,T,\sigma_{BS}(K,T)) ，我们得到

D(K,T)=-\frac{\partial C_{BS}(K,T,\sigma_{BS}(K,T))}{\partial K}\\ =-\frac{\partial C_{BS}}{\partial K}-\frac{\partial C_{BS}}{\partial\sigma_{BS}}\frac{\partial\sigma_{BS}}{\partial K}=-\frac{\partial C_{BS}}{\partial K}-\mathrm{Vega}\times\mathrm{skew}\\

这里Vega衡量的是期权价格关于随波动了率变化的敏感程度。

Black-Scholes模型还可以被用于交换期权（exchange option）的定价。假设两个无股息支付的股票遵循

dX_t=\mu_xX_tdt+\sigma_xX_tdW_t^x\\ dY_t=\mu_yY_tdt+\sigma_yY_tdW_t^y\\

且 dW_t^xdW_t^y=\rho dt 。令 Z_t=\frac{Y_t}{X_t} ，根据伊藤引理，

\frac{dZ_t}{Z_t}=(\mu_y-\mu_x-\rho\sigma_x\sigma_y+\sigma_x^2)dt+\sigma_ydW_t^y-\sigma_xdW_t^x\\

\frac{dZ_t}{Z_t} 的瞬时方差（instantaneous variance）是 (\frac{dZ_t}{Z_t})^2=(\sigma_ydW_t^y-\sigma_xdW_t^x)^2=(\sigma_x^2+\sigma_y^2-2\rho\sigma_x\sigma_y)dt 。定义 \sigma^2=\sigma_x^2+\sigma_y^2-2\rho\sigma_x\sigma_y ，并定义过程 W_t ，使其满足

dW_t=\frac{\sigma_y}{\sigma}dW_t^y-\frac{\sigma_x}{\sigma}dW_t^x\\

由于 (dW_t)^2=(\frac{\sigma_ydW_t^y-\sigma_xdW_t^x}{\sigma})^2=dt ，根据莱维特征标记定理（Levy's characterization theorem）， W_t 是一个布朗运动。这样， Z_t 就是一个几何布朗运动，它在原始概率测度下满足

dZ_t=\mu Z_tdt+\sigma Z_tdW_t\\

其中 \mu=\mu_y-\mu_x-\rho\sigma_x\sigma_y+\sigma_x^2 。

在到期时间 T ，交换期权的回报是 \max(Y_T-X_T,0) ，所以鞅（martingale）定价给出的其在时间 0 的价格为 P_t=\mathbb{E}^Q_t[\max(Y_T-X_T,0)] ，这里 Q 是原始概率测度。此条件期望（conditional expectation）可以直接计算，但过程会比较冗长。一个更简单的方法是用计价物变换（change of numeraire）。若我们以 X_t 为计价物，并令 Q_x 为相应的概率测度，鞅定价给出

\frac{P_t}{X_t}=\mathbb{E}^{Q_x}_t\left[\frac{\max(Y_T-X_T,0)}{X_T}\right]=\mathbb{E}^{Q_x}_t[\max(Z_T-1,0)]\\

我们知道 Z_t 在原始测度下的动态，而根据吉尔萨诺夫定理（Girsanov's theorem），测度变换后，只有漂移项会变，而波动率不会变。又因为 Z_t 在测度 Q_x 下是一个鞅，其在测度 Q_x 下的漂移项为 0 。那么 \mathbb{E}^{Q_x}_t[\max(Z_T-1,0)]\ 就变成了无风险利率为 0 、成交价为 1 的Black-Scholes期权价格，即

P_t=X_tN(-d_2)-Y_tN(-d_1)\\ d_1=\frac{\ln(Y_t/X_t)+\sigma^2(T-t)/2}{\sigma\sqrt{T-t}}\\ d_2=d_1-\sigma\sqrt{T-t}=\frac{\ln(Y_t/X_t)-\sigma^2(T-t)/2}{\sigma\sqrt{T-t}}\\

6 远期合约和Black公式

若令 F_t=S_te^{(r-q)(T-t)} 为在到期时间 T 交割的股票远期合约（forward）在时间 t 的价格，那么欧式看涨期权的Black-Scholes公式可被写为

C(F,t)=e^{-r(T-t)}F_tN(d_1)-e^{-r(T-t)}KN(d_2)\\ d_1=\frac{\ln(F_t/K)+\sigma^2(T-t)/2}{\sigma\sqrt{T-t}}\\ d_2=d_1-\sigma\sqrt{T-t}=\frac{\ln(F_t/K)-\sigma^2(T-t)/2}{\sigma\sqrt{T-t}}\\

当期权价格写作关于远期价格（forward price）而非现价（spot price）的函数时，期权价格的公式被称作Black公式，它强调了远期价格在期权定价中的重要性。注意在Black公式中，期权价格被表达为以无风险利率折现的期权预期回报。

Black-Scholes模型很容易应用各类衍生品的定价。当然，在所有这些情况下，人们都很清楚，该模型有许多缺点。因此该模型在很多方面得到了改进，改进后的包括跳跃扩散（jump diffusion）模型、随机波动率（stochastic volatility）模型、局部波动率（local volatility）模型等。Black-Scholes模型的主要用途之一是通过隐含波动率为衍生品报价（quote price）。即使对于不遵循几何布朗运动的证券，人们也会这样做。

参考文献

[1] Kerry Back. A Course in Derivative Securities: Introduction to Theory and Computation.

[2] Tomas Bjork. Arbitrage Theory in Continuous Time.

[3] Steven E. Shreve. Stochastic Calculus for Finance II-Continuous-Time Models. Springer Finance. Springer, New York, 2004.